Work Energy And Power
- Work – when a force is applied to an object and object moves in direction of force.
Formula: Work = Force × Distance × cos(θ), Unit: Joules (J) - Energy – The capacity to do work. There are many forms (kinetic, potential, thermal, etc.).
Unit: Joules (J) - Power – The rate at which work is done or energy is transferred.
Formula: Power = Work / Time, Unit: Watts (W)
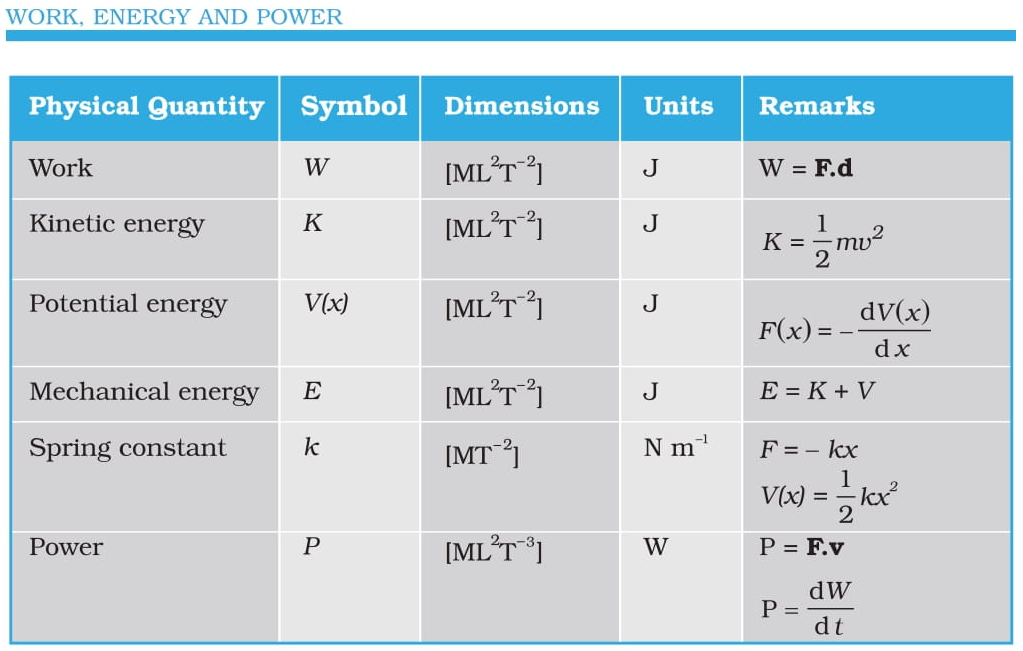
Scientific Conception Of Work
The two conditions need to be satisfied for work to be done: (i) a force should act on an object, and (ii) the object must be displaced. If any one of the above conditions does not exist, work is not done. This is the way we view work in science.
Work Done = Force × Displacement × cos(θ) [W=Fs × cos(θ)] Where, (angle between force & displacement, same direction)
- Work done by a force acting on an object is equal to the magnitude of the force multiplied by the distance moved in the direction of the force.
- Work has only magnitude and no direction.
- In Eq., if F= 1 N and s = 1 m then the work done by the force will be 1 Nm. Here the unit of work is newton metre (Nm) or joule (J).
- Thus 1 J is the amount of work.
- the work done by a force can be either positive or negative depends on the force is in the direction of displacement.
The energy possessed by an object is thus measured in terms of its capacity of doing work. [Unit of energy is, joule (J)] 1 J is the energy required to do 1 joule of work. Energy in many different forms include Mechanical Energy (Potential Energy + Kinetic Energy), heat energy, chemical energy, electrical energy and light energy. [KE = 1/2 mv², PE = mgh]
The potential energy of an object at a height depends on the ground level or the zero level you choose. An object in a given position can have a certain potential energy with respect to one level and a different value of potential energy with respect to another level.
The Story behind unit of energy and work called joule
James Prescott Joule (1818-1889) was a British physicist. He is best known for his research in electricity and thermodynamics. he formulated a law for the heating effect of electric current. He also verified experimentally the law of conservation of energy and discovered the value of the mechanical equivalent of heat.
Law Of Conservation Of Energy
The form of energy can be changed from one form to another, the total energy remains unchanged. According to this law,
- Energy can only be converted from one form to another, it can neither be created or destroyed.
- The total energy before and after the transformation remains the same.
- The law of conservation of energy is valid in all situations and for all kinds of transformations.
We find that during the free fall of the object, the decrease in potential energy, at any point in its path, appears as an equal amount of increase in kinetic energy. There is thus a continual transformation of gravitational potential energy into kinetic energy.
Power measures the speed of work done, that is, how fast or slow work is done. Power is defined as the rate of doing work or the rate of transfer of energy. [Power = work/time ог P = W/t] The unit of power is watt [in honour of James Watt (1736-1819)] having the symbol W. 1 watt is the power of an agent, which does work at the rate of 1 joule per second.
We can also say that power is 1 W when the rate of consumption of energy is 1J * s ^ – 1
1 watt = 1 joule/second or IW = 1 J * s ^ – 1, We express larger rates of energy transfer in kilowatts (kW). 1 kilowatt = 1000 watts, 1kW = 1000W, 1kW = 1000J * s ^ – 1
Therefore the concept of average power is useful. We obtain average power by dividing the total energy consumed by the total time taken.
Alternative Units of Work/Energy in J
- erg – 10 ^ – 7 J
- electron volt (eV) 1.6 * 10 ^ – 19 J
- calorie (cal) 4.186 J
- kilowatt hour (kWh) 3.6 * 10 ^ 6 J
What you have learnt
- Work done on an object is defined as the magnitude of the force multiplied by the distance moved by the object in the direction of the applied force. The unit of work is joule: 1 joule 1 newton x 1 metre.
- Work done on an object by a force would be zero if the displacement of the object is zero.
- An object having capability to do work is said to possess energy. Energy has the same unit as that of work.
- An object in motion possesses what is known as the kinetic energy of the object. An object of mass, m moving with moving w velocity v has a kinetic energy of mv² 2
- The energy possessed by a body due to its change in position or shape is called the potential energy. The gravitational potential energy of an object of mass, m raised through a height, h from the earth’s surface is given by m gh.
- According to the law of conservation of energy, energy can only be transformed from one form to another; it can neither be created nor destroyed. The total energy before and after the transformation always remains constant.
- Energy exists in nature in several forms such as kinetic energy, potential energy, heat energy, chemical energy etc. The sum of the kinetic and potential energies of an object is called its mechanical energy.
- Power is defined as the rate of doing work. The SI unit of power is watt. 1 W = 1 J/s.
Question
Q1) A force of 5 N is acting on an object. The object is displaced through 2 m in the direction of the force. If the force acts on the object all through the displacement, then work done is 5 N * 2m = 10 Nm or 10 J.
Q2) A porter lifts a luggage of 15 kg from the ground and puts it on his head 1.5 m above the ground. Calculate the work done by him on the luggage. [Solution: Work done is 225 J.]
Q3) A pair of bullocks exerts a force of 140 N on a plough. The field being ploughed is 15 m long. How much work is done in ploughing the length of the fiel?
Q4) An object of mass 15 kg is moving with a uniform velocity of 4 ms⁻¹ What is the kinetic energy possessed by the object?
Q5) What is the work to be done to increase the velocity of a car from 30km * h ^ – 1 to 60km * h ^ – 1 if the mass of the car is 1500 kg?
Q6) Find the energy possessed by an object of mass 10 kg when it is at a height of 6 m above the ground. Given, g=9.8 m/s2
Q7) An object of mass 12 kg is at a certain height above the ground. If the potential energy of the object is 480 J, find the height at which the object is with respect to the ground. Given, g=9.8 m/s2
Q8) Two girls, each of weight 400 N climb up a rope through a height of 8 m. We name one of the girls A and the other B. Girl A takes 20 s while B takes 50 s to accomplish this task. What is the power expended by each girl?
Q9) A boy of mass 50 kg runs up a staircase of 45 steps in 9 s. If the height of each step is 15 cm, find his power. Take g = 10m * s ^ – 2
